zurück

DAS DREIECK

 

 

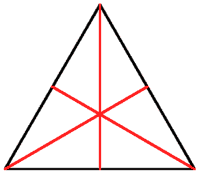
 Beim gleichseitigen Dreieck sind die Seitenhalbierenden identisch mit den Höhen und den Winkelhalbierenden. Der gemeinsame Schnittpunkt (Schwerpunkt) teilt diese jeweils im Verhältnis 1:2.

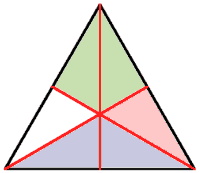
Als Teilfiguren entstehen Drachenvierecke, rechtwinklige Dreiecke und gleichseitige Dreiecke.

 

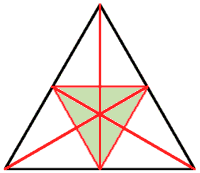
 Aus der Verbindung der Seitenmitten ergibt sich eine Aufteilung in vier wiederum gleichseitige Dreiecke mit halber Seitenlänge.

 

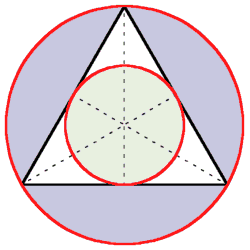
 Mit dem Schwerpunkt als Mittelpunkt lässt sich ein In- und ein Umkreis zeichnen, deren Radien im Verhältnis 1:2 zueinander stehen. Der Inkreis halbiert den längeren Teil der Seitenhalbierenden, sodass diese dadurch auf einfache Weise gedrittelt wird.

Mittels der Schnittpunkte des Inkreises mit den Seitenhalbierenden lässt sich eine Unterteilung in 9 kongruente Teildreiecke konstruieren.

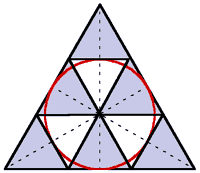
Aus jeweils zwei Teildreiecken lassen sich Parallelogramme zusammensetzen.

 

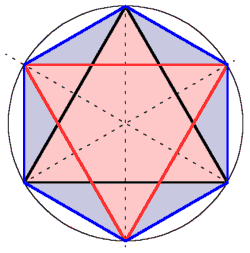
 Die Verlängerungen der Seitenhalbierenden schneiden den Umkreis in drei Punkten, aus denen sich nun ein reguläres Sechseck oder ein Sechsstern ergänzen lässt.

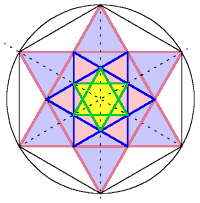
Das um 180 Grad gedrehte Ausgangsdreieck bildet mit ersterem als Schnittfläche wiederum ein Sechseck. Durch Verbindung der übernächsten Punkte können aus diesem unendlich viele und immer kleinere Sechssterne abgeleitet werden.

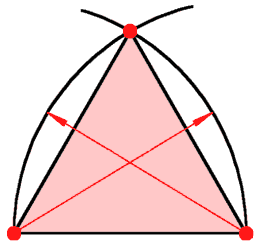
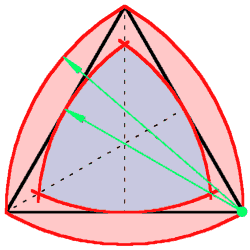
Betrachten Sie ein aus dieser Figur gebildetes Parkett!

 

Kreisbögen um die Ecken ergeben sphärische Dreiecke. Das größere hat als Radius die Seitenlänge, das kleinere die Höhe.

 

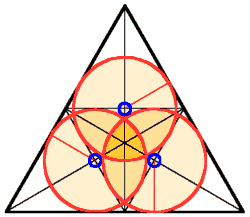
 Die Schnittpunkte der Höhen mit den jeweiligen Verbindungen der Seitenmitten sind Mittelpunkte dreier einbeschriebener Kreise. Der Radius entspricht dem Lot von den Mittelpunkten auf die Dreiecksseiten.

 

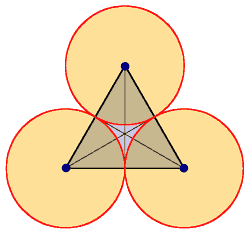
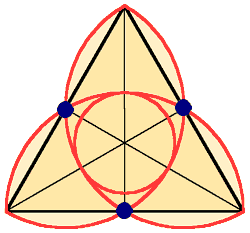
 Dieser einfache Dreipass entsteht aus Kreisen mit den Ecken als Mittelpunkten und der halben Seitenlänge als Radius. Alternativ kann der Radius auch am Schwerpunkt ausgerichtet werden (rechts). Dadurch entstehen Überschneidungen zwischen den Kreisen. 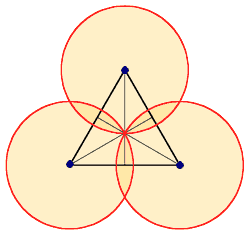Betrachten Sie ein aus dieser Figur gebildetes Parkett!
Betrachten Sie ein aus dieser Figur gebildetes Parkett! Kreisbögen um die Seitenmittelpunkte ergeben diese Figur, bei der in der Mitte ein sphärisches Dreieck als gemeinsame Schnittmenge entsteht.