Polygon - Hexagon

zurück
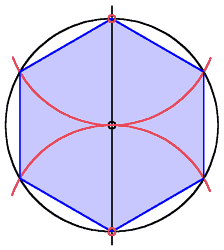
DAS SECHSECK (Hexagon)
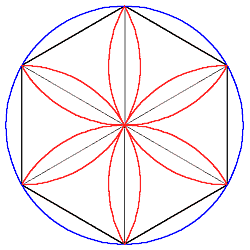
	Der Umfang eines Kreises lässt sich mit seinem Radius in sechs gleiche Teile teilen. Aus den Radien in allen Ecken entsteht eine solche Blütenform.
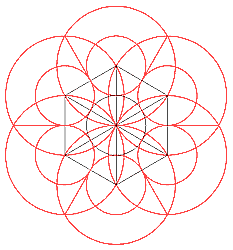
	Die Kreise um die Ecken mit halber oder ganzer Seitenlänge als Radius ergeben einen gotischen Sechspass.
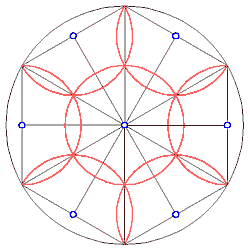
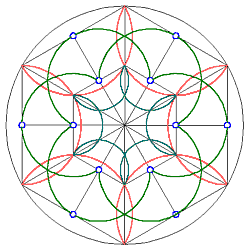
	Kreisbögen um die Seitenmitten mit halbem Radius (links). Weitere Kreisbögen auf sich hieraus ableitbaren Punkten differenzieren die Figur und veranschaulichen interessante Regelmäßigkeiten (rechts).
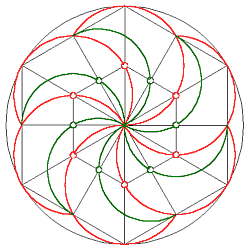
	Kreisbögen um die Mitten der Strahlen zu den Ecken und den Seitenmitten ergeben diese leicht zu konstruierende Spiralform.
	Wenn jeder zweite Punkt mit geraden Linien verbunden wird, ergeben zwei gleichseitige Dreiecke einen sechszackigen Stern.
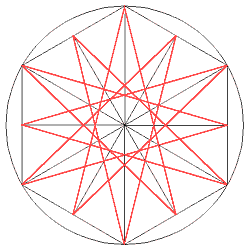	Die Seitenmitten werden mit den Ecken der gegenüberliegenden Seiten verbunden und bilden so einen zwölfstrahligen Stern mit unterschiedlichen Zackenlängen. In der Mitte entsteht ein reguläres Zwölfeck.
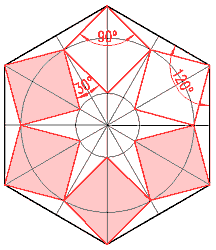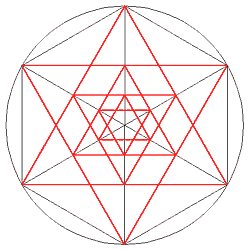
	In den Ecken eingepasste Quadrate, deren Diagonalen mit den Durchmessern des Sechsecks zusammenfallen. In der Mitte wird ein sechsstrahliger Stern ausgespart.
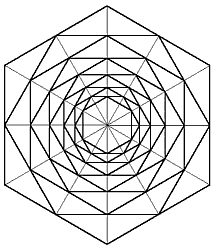	Die Verbindung der Seitenmitten ergibt jeweils wieder Sechsecke, die wechselweise um 30 Grad gedreht sind.